開校時間 | 平日16:00~21:40 祝日14:00~19:00 |
|---|
定休日 | 土曜※・日曜 土曜は不定期開校 |
|---|
対象学年 | 中学生(市内公立中) 高校生 |
|---|
1問解けるようになること
2016年07月18日
1問解けるようになることがどれほど大切なことか、一体どれくらいの子が認識できているのでしょうか。
逆に、1問解けないまま放置しておくことが、どれほど勿体ないことか、どれくらいの子が認識できているのでしょうか。
当然ですが、入試や模試で出て来る問題は今まで世に出てきたことの無い問題であり、どの問題集にも全く同じ問題は掲載されていません。定期テストのように、課題と全く同じ問題が出てきたり、ちょっと数字が変わっただけのようなものではありません。
このような完全に初見の問題を解くことができるのは、どのような子か。
それは、「この問題と似た問題は見たことある!」「この出題のときの解くパターンは知っている!」というように気付くことができる子です。
では、そう気付くことが出来るようになるためにはどうするか。
当然いろいろな問題に触れておかなくてはいけません。そして触れた問題は完全に解くことができるようになっていなければいけません。
定期テストでも、この問題を解いたことは覚えているけど、解き方は忘れた…という経験はありませんか?解いたことある、という経験だけ持っていても入試では役に立ちません。実際解くことができて初めて類題に生かすことができるのです。
しかしすべての問題を完全に解けるようになるにはかなりの苦労を要します。例えば高校生の参考書チャート式(青)ⅠAⅡBの総問題数は約1600~1700問です。この数の問題を完璧に解けるようになるには、かなりの時間と根気が必要です。私もチャート式をすべて解き切ることはできませんでした。
ではどうやって限られた時間にいろいろな問題に触れ、かつ1問1問完璧に理解できるようにするのか。
はっきり言ってそんなことは無理です。1700問を完璧に解けるようになればそれはかなりの武器になりますが、それができれば苦労しません。1教科あたりに費やせる時間は限られています。1教科に、悠長に時間を使っている暇など受験期にはありません。
入試で出題されるであろう問題すべてを「一度解いたことがある問題」にすることは不可能です。だからこそ、1問完璧に解けるようになることが重要なのです。
1問を完璧に解くことができる、ということはその背後にある何百の問題を解くためのヒントを得たことになります。
これが入試においてどれほど価値のあることか。
「この問題は、あの問題の解き方を使えば解けるんじゃないか?」「こう聞かれたら、こう解く、というパターンあったよな…」
このような気付きが合否を分けることになります。
逆に1問をできないまま放置すれば、その背後にある何百と言う問題を解けないまま放置したことになるのです。
夏休みに入りますが、中学生は前期中間テスト、高校生は1学期中間期末テストをもう一度解き直して見てください。自信を持って100点取れると言えますか?
一度直しをしている問題ですから、解けて当然なわけです。にも関わらず、解き直しで100点取れなかった子は、解けない問題を放置していることになります。それが何を意味しているかは前述した通りです。
テストごとに1問1問完璧に解けるようにしていく。その積み重ねが受験のときに、大きな力となって皆さんをサポートしてくれます。
たかが一問、されど1問。
これを肝に銘じて、夏休みにしっかり復習を進めていきましょう!
2025年度定員情報
塾全体の定員に達した場合は募集を停止致します。興味のある方はお早めにお問い合わせください。
中1…募集停止
中2…募集停止
中3…募集終了
高1…1~2人
高2…1~2人
高3…募集終了
お問い合わせ

フォームでのお問い合わせは24時間受け付けております。お気軽にご連絡ください。
LINEでお問い合わせ
友達追加をして、お気軽にお問い合わせください!
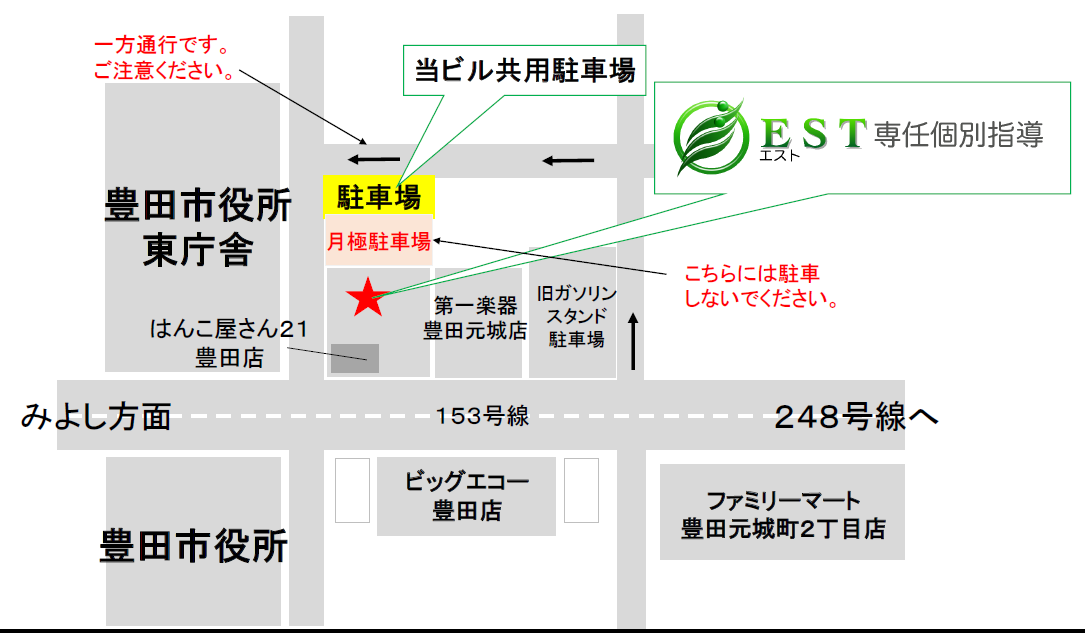
アクセス
住所
〒471-0024
愛知県豊田市元城町4-19-1名古庄ビル2階
豊田市駅から徒歩7分
駐輪場あり
ビル共用駐車場あり
詳細図
営業時間
平日16:00~21:40
祝日※14:00~19:00
メールでのお問合せは24時間受け付けております。
※講習期間を除きます。
規定休校日
土曜・日曜 / 年末年始・お盆・GW
※土曜不定期開校(月間予定表)